3.1 퍼셉트론에서 신경망까지

은닉층
- 입력층이나 출력층과 달리 사람 눈에는 보이지 않는다

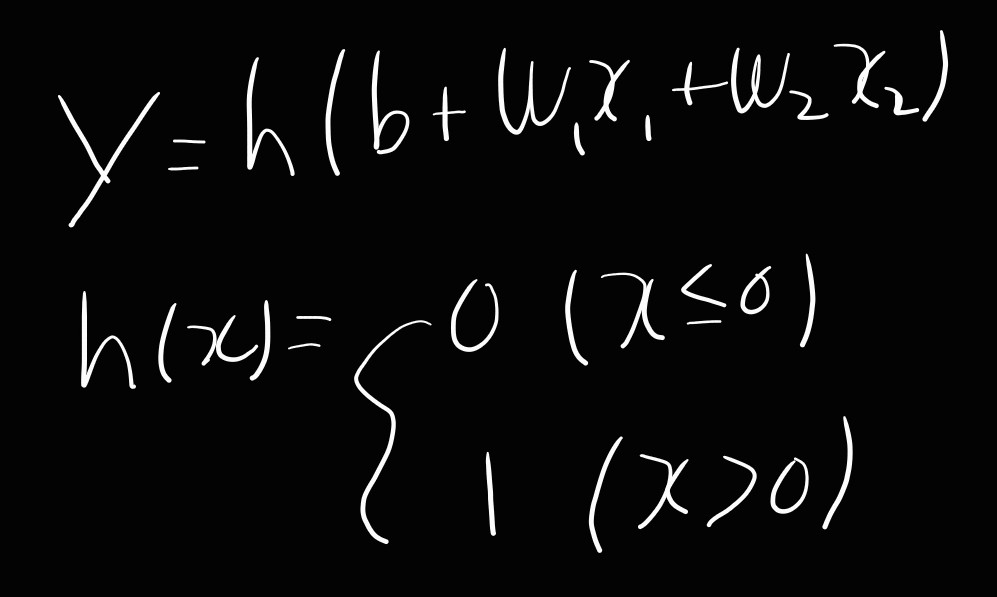
활성화 함수
- 위와 같이 입력 신호의 총합을 출력 신호로 변환하는 함수(h(x))를 활성화 함수라고 부른다
- 이를 수식과 뉴런으로 표현하면 아래와 같다

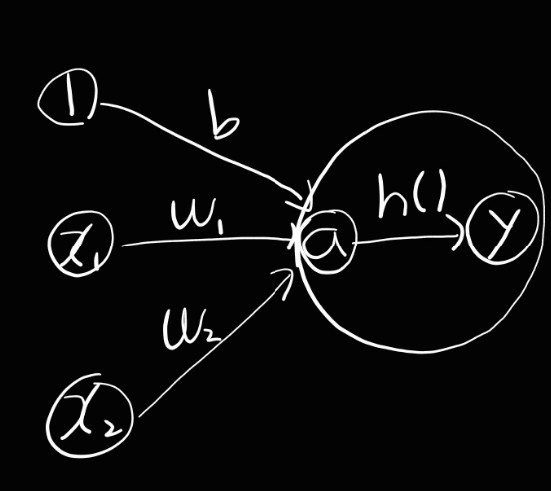
뉴턴의 그림
- 보통 뉴턴을 그릴 때는 왼쪽과 같고 활성화 처리 과정은 오른쪽과 같다

계단 함수(step function)
- 임계값을 경계로 출력이 바뀌는 함수를 계단 함수라고 한다
시그모이드 함수(sigmoid funcion)
- 신경망에서 자주 이용하는 활성화 함수이다
- 식은 아래와 같다
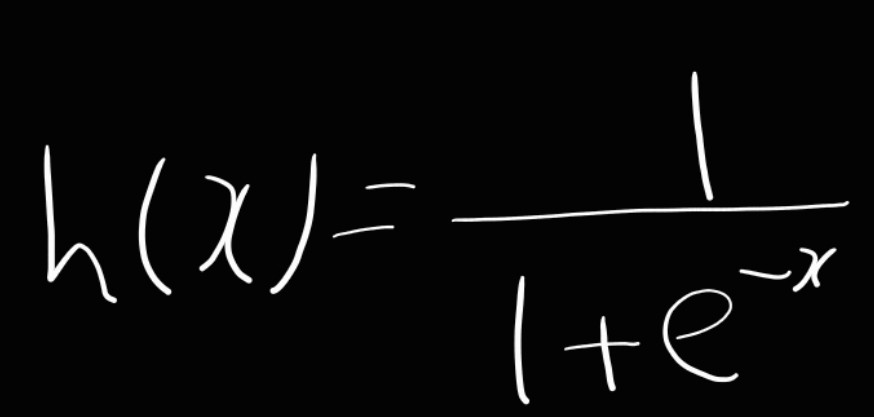
- 신경망에서는 활성화 함수로 시그모이드 함수를 이용하여 신호를 변환하고, 그 변환된 신호를 다음 뉴런에 전달한다
계단 함수 구현
import numpy as np
def step_function(x):
y=x>0
return y.astype(np.int64)
x=np.array([-1,1,2])
print(step_function(x))- 인수 x는 실수만 받아들이기 때문에 넘파이 배열을 인수로 넣기 위해서는 넘파이 배열에 부등호 연산을 수행하여 bool q배열을 생성하고 bool에서 int형으로 바꾸어 계단 함수를 만들어준다
- 넘파이 배열의 자료형을 변환할 때는 astype() 메서드를 이용한다
계단 함수 그래프
import numpy as np
import matplotlib.pylab as plt
def step_function(x):
return np.array(x>0, dtype=np.int64)
x=np.arange(-5.0,5.0,0.1)
y=step_function(x)
plt.plot(x,y)
plt.ylim(-0.1,1.1)
plt.show()
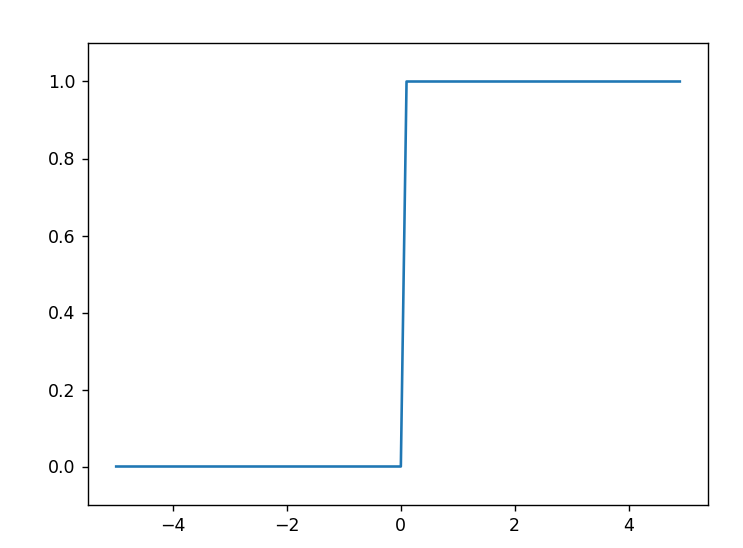
시그모이드 함수 구현 및 그래프
import numpy as np
import matplotlib.pylab as plt
def sigmoid(x):
return 1/(1+np.exp(-x))
x=np.arange(-5.0,5.0,0.1)
y=sigmoid(x)
plt.plot(x,y)
plt.ylim(-0.1,1.1)
plt.show()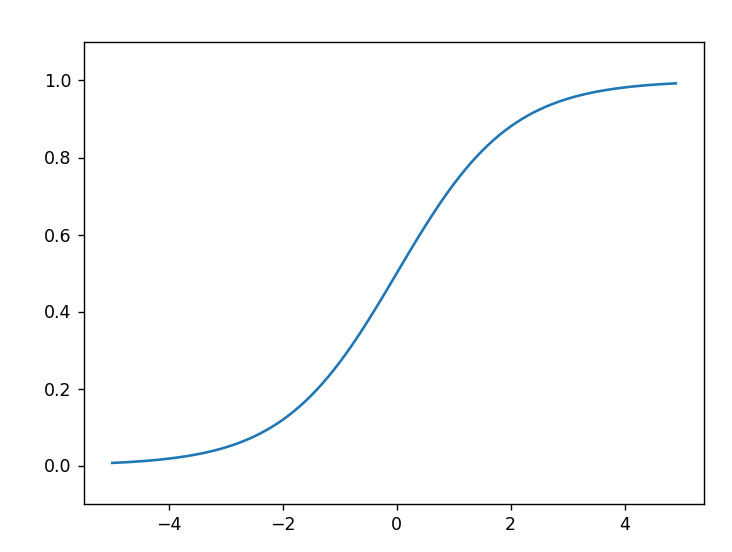
계단 함수와 시그모이드 함수 차이점
- 시그모이드 함수는 부드러운 곡선이며 입력에 따라 출력이 연속적으로 변화하지만 계단 함수는 0을 경계로 출력이 갑자기 바뀌어버린다.
- 계단 함수는 0과 1 중 하나의 값만 돌려주는 반면 시그모이드 함수는 실수를 돌려준다
계단 함수와 시그모이드 함수 공통점
- 큰 관점에서 보면 입력이 작을 때의 출력은 0에 가깝고 입력이 커지면 1에 가까워지는 구조이다
- 비선형 함수이다
비선형 함수
- 출력이 입력의 상수배만큼 변하는 함수를 선형 함수라고 부르는데 그 외를 비선형 함수라고 부른다
선형 함수의 문제점
- 층을 깊게 해도 '은닉층이 없는 네트워크'로도 똑같은 기능을 할 수 있다
- e.g.) 활성화 함수를 h(x)=cx 라고 할 때 이를 3층 네트워크로 나타낸다고 하면 y=(h(h(h(x))))가 된다.
y=c*c*c*x 처럼 수행하지만 y=ax와 같은 식으로 a=c^3 일 뿐이다
ReLU 함수
- 최근에 사용하는 활성화 함수이다
- 입력이 0을 넘으면 그 입력을 그대로 출력하고, 0 이하이면 0을 출력하는 함수이다
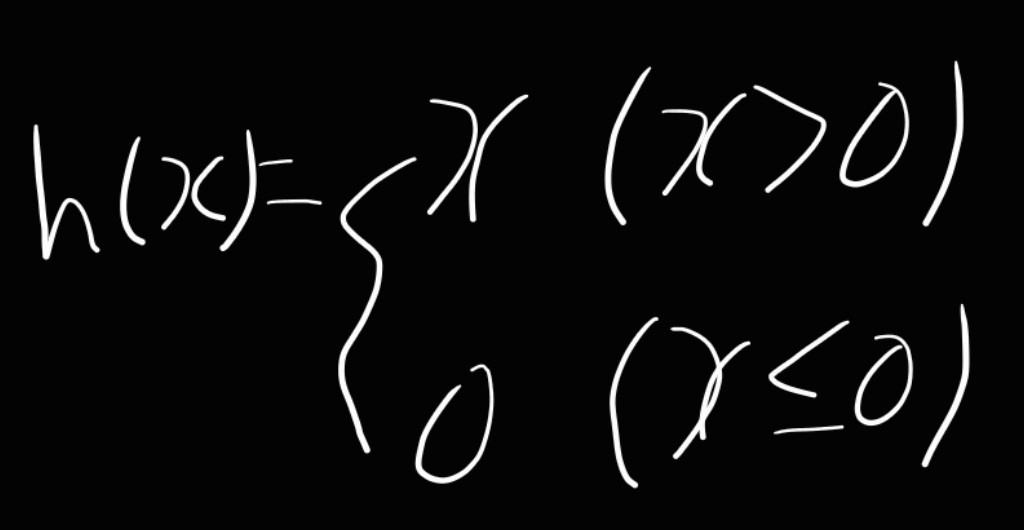
- 아래는 ReLU 함수 구현과 그래프이다.
import numpy as np
import matplotlib.pylab as plt
def relu(x):
return np.maximum(0,x)
x=np.arange(-5.0,5.0,0.1)
y=relu(x)
plt.plot(x,y)
plt.ylim(-0.1,1.1)
plt.show()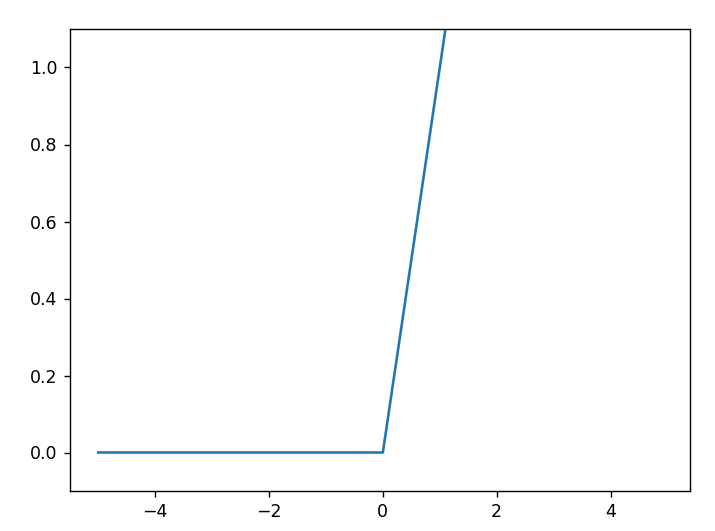
3.3 다차원 배열의 계산
다차원 배열
import numpy as np
B=np.array([[1,2],[3,4],[5,6]])
print(B)
print(np.ndim(B)) # 차원 수
print(B.shape) # 배열의 형상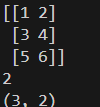
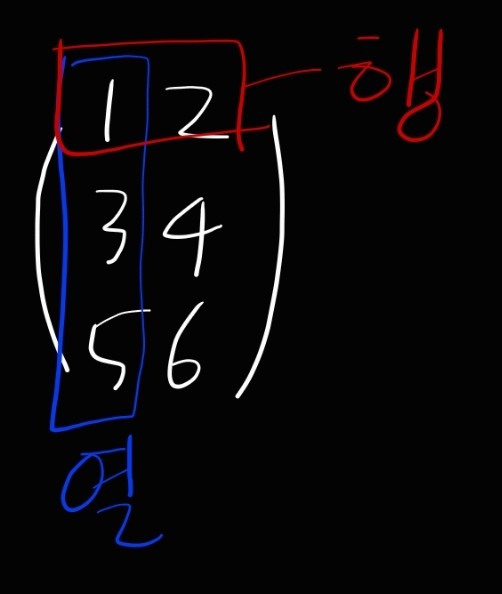
- 2차원 배열은 행렬이라고 부른다
- 배열의 가로 방향은 행(row), 세로 방향은 열(column)이라고 부른다
행렬의 곱
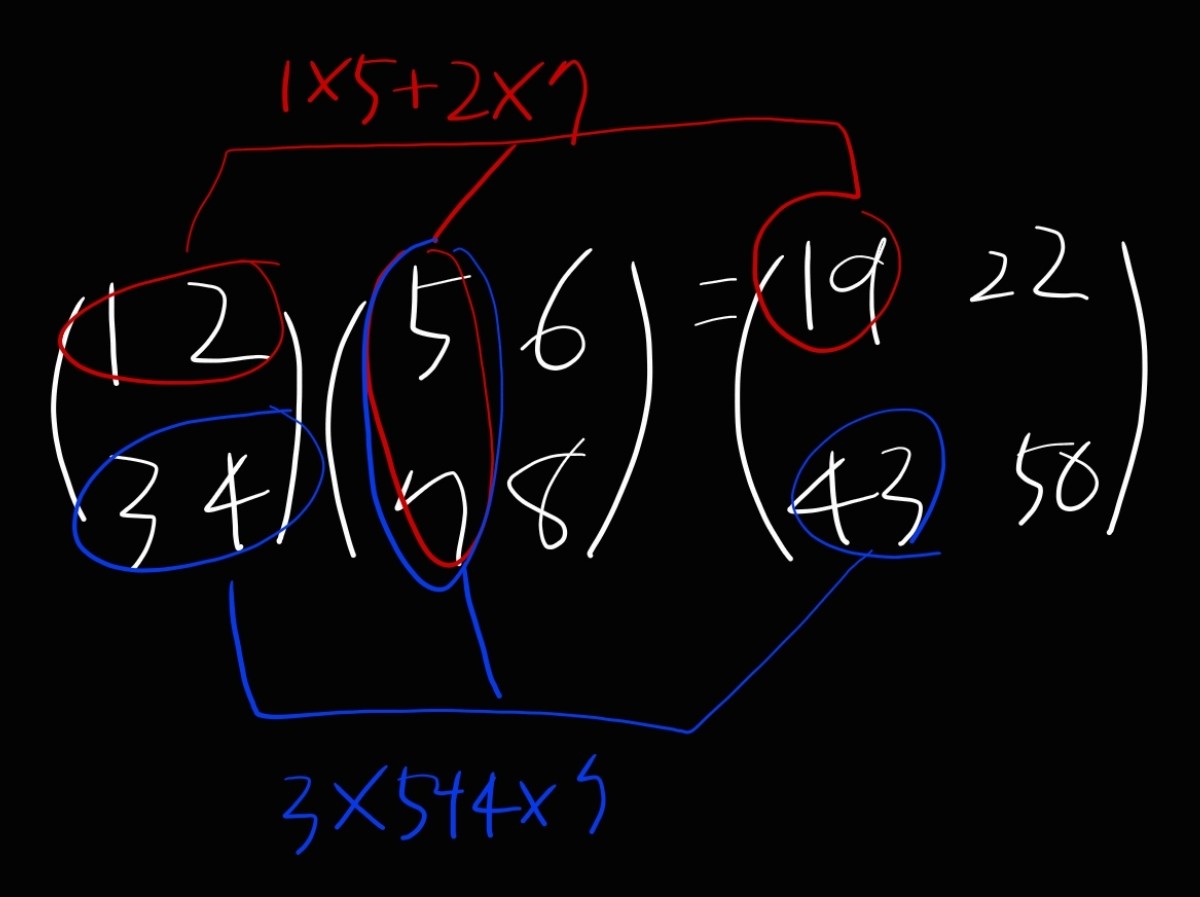
import numpy as np
A=np.array([[1,2],[3,4]])
B=np.array([[5,6],[7,8]])
print(np.dot(A,B))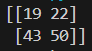
- 함수 np.dot()dms 1차원 배열이면 벡터를, 2차원 배열이면 행렬 곱을 계산한다
- 순서가 바뀌면 결과값이 달라진다(교환법칙이 성립되지 않는다)
- 행렬의 곱을 하기 위해서는 행렬의 형상에 유의해야 한다
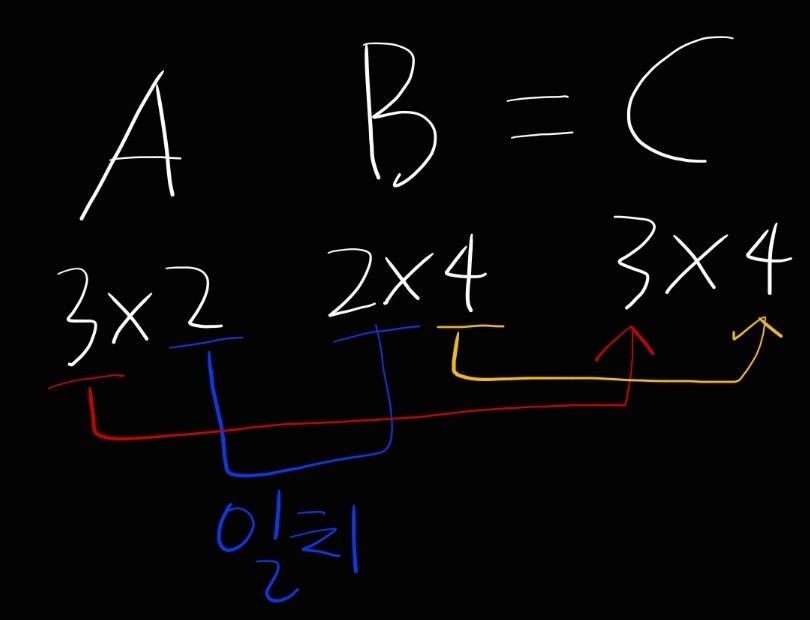
- 일치시켜야하는 부분에 일치해야 계산할 수 있다.
> 3x3 2x4 로 계산하면 오류가 난다
신경망에서의 행렬 곱
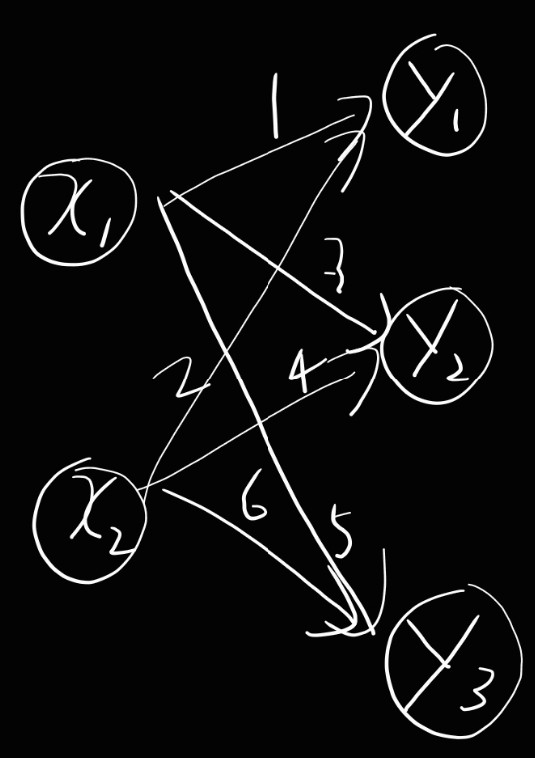
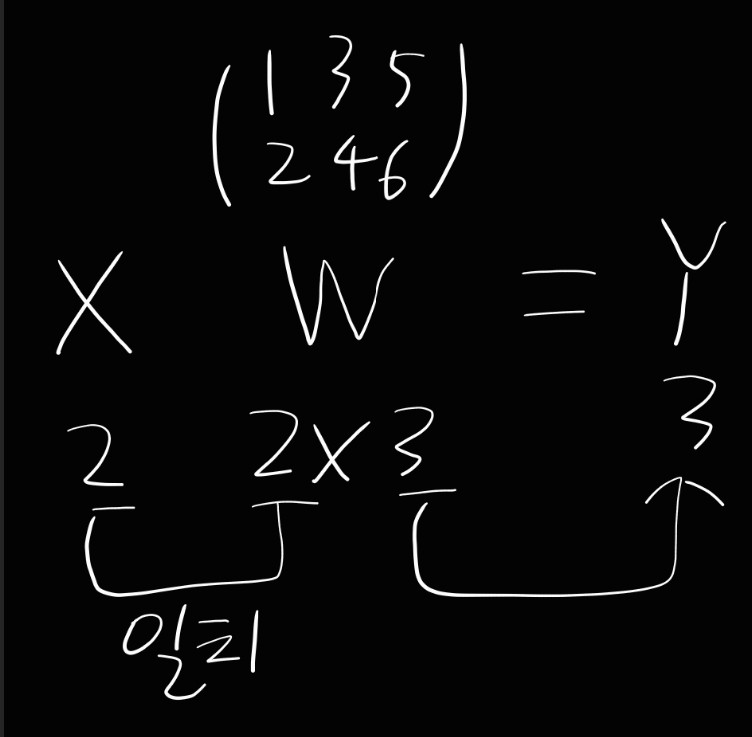
- 이를 구현하면 아래와 같다
import numpy as np
X=np.array([1,2])
print(X.shape)
W=np.array([[1,3,5],[2,4,6]])
print(W.shape)
Y=np.dot(X,W)
print(Y)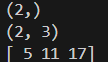
3층 신경망
- 입력층(0층) 2개, 첫 번째 은닉층(1층)은 3개, 두 번째 은닉층(2층)은 2개, 출력층(3층) 3개의 뉴런으로 구성된
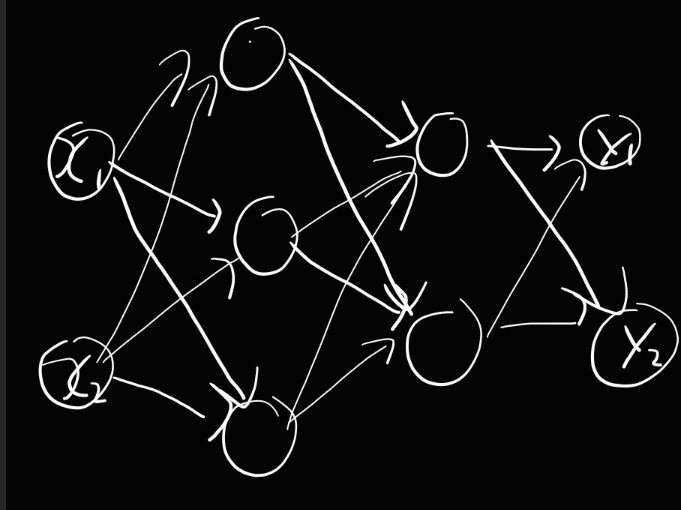
표기법
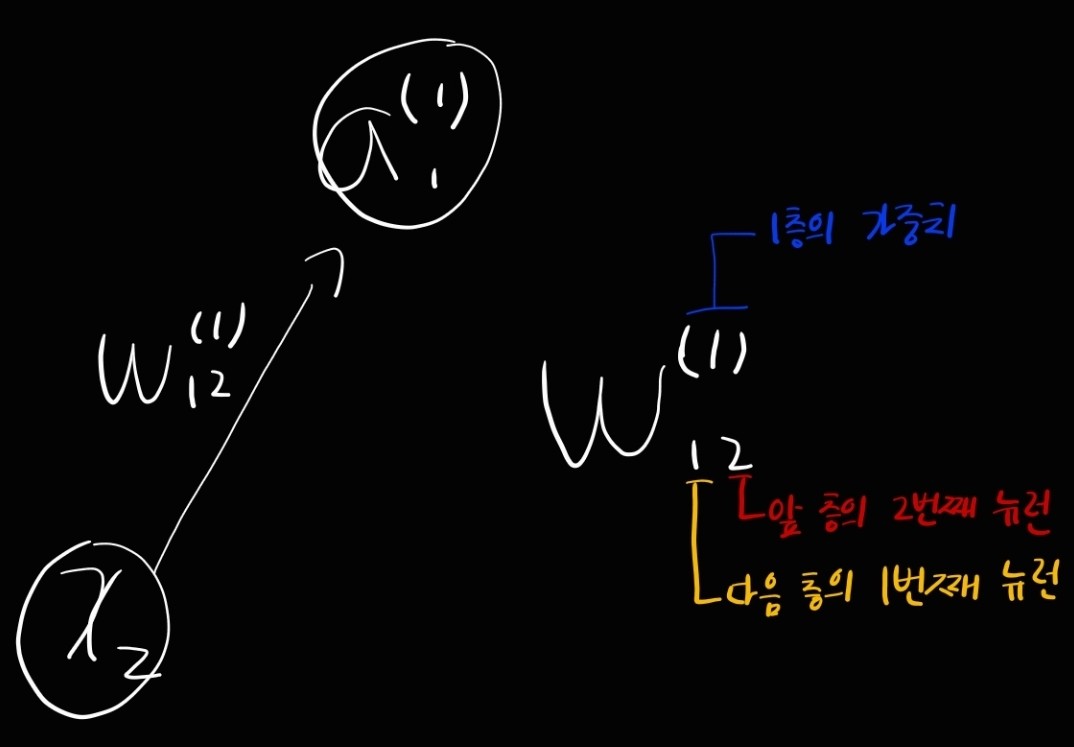
각 층의 신호 전달 구현하기
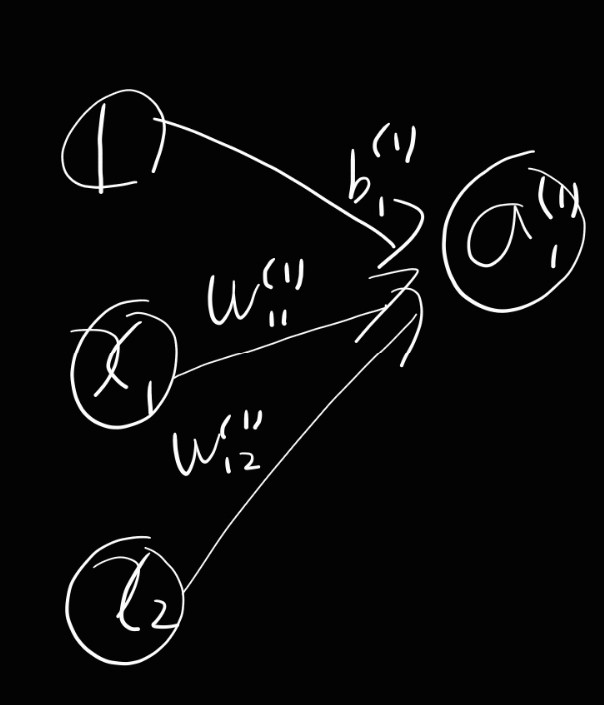
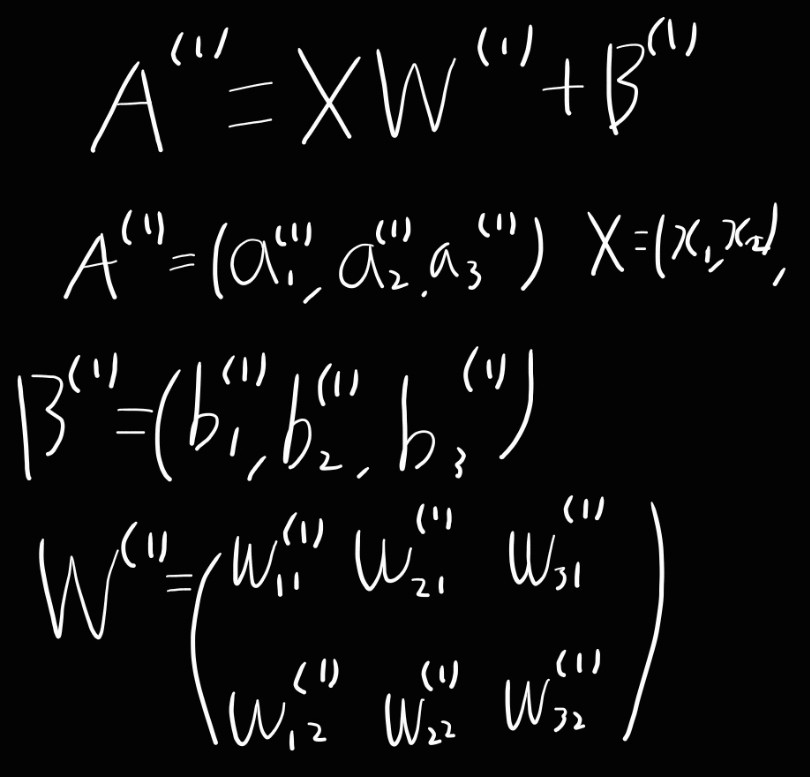
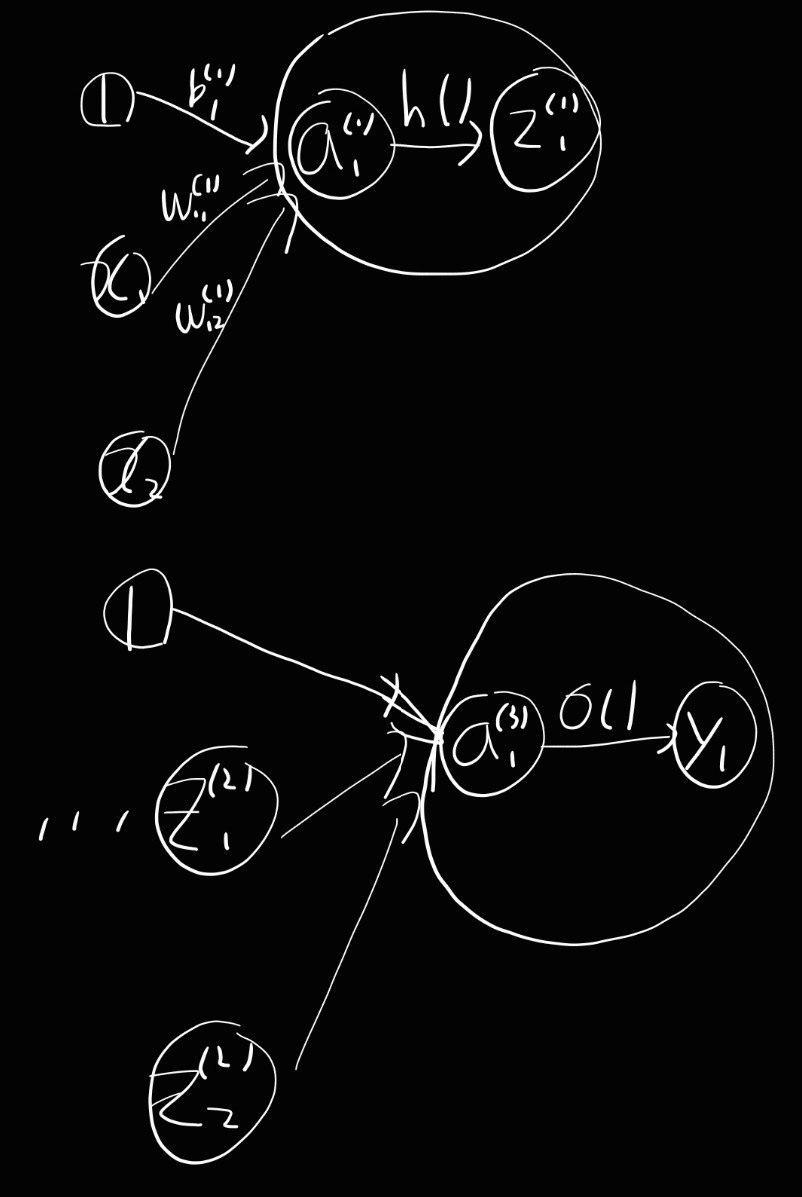
3층 신경망 구현
import numpy as np
# 시그모이드 함수
def sigmoid(x):
return 1/(1+np.exp(-x))
# 항등 함수 (출력층의 활성화 함수)
def identity_function(x):
return x
# 가중치와 편향을 초기화 및 딕셔너리 저장
def init_network():
network={}
network['W1']=np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
network['b1']=np.array([0.1,0.2,0.3])
network['W2']=np.array([[0.1,0.4],[0.2,0.5],[0.3,0.6]])
network['b2']=np.array([0.1,0.2])
network['W3']=np.array([[0.1,0.3],[0.2,0.4]])
network['b3']=np.array([0.1,0.2])
return network
# 순방향으로 전달됨을 알리기 위함
def forward(network,x):
W1,W2,W3=network['W1'],network['W2'],network['W3']
b1,b2,b3=network['b1'], network['b2'], network['b3']
a1=np.dot(x,W1)+b1
z1=sigmoid(a1)
a2=np.dot(z1,W2)+b2
z2=sigmoid(a2)
a3=np.dot(z2,W3)+b3
y=identity_function(a3)
return y
network=init_network()
x=np.array([1.0,0.5])
y=forward(network,x)
print(y)
'학교 공부 > 컴퓨터비전' 카테고리의 다른 글
| 밑바닥부터 시작하는 딥러닝 Chapter 4 : 신경망 학습 (0) | 2024.05.02 |
|---|---|
| 밑바닥부터 시작하는 딥러닝 Chapter3-2 : 신경망 (0) | 2024.05.02 |
| 밑바닥부터 시작하는 딥러닝 Chapter2 : 퍼셉트론 (0) | 2024.05.01 |
| 밑바닥부터 시작하는 딥러닝 Chapter1 : 헬로 파이썬 (0) | 2024.04.29 |



