주소 : https://www.acmicpc.net/problem/1085
1085번: 직사각형에서 탈출
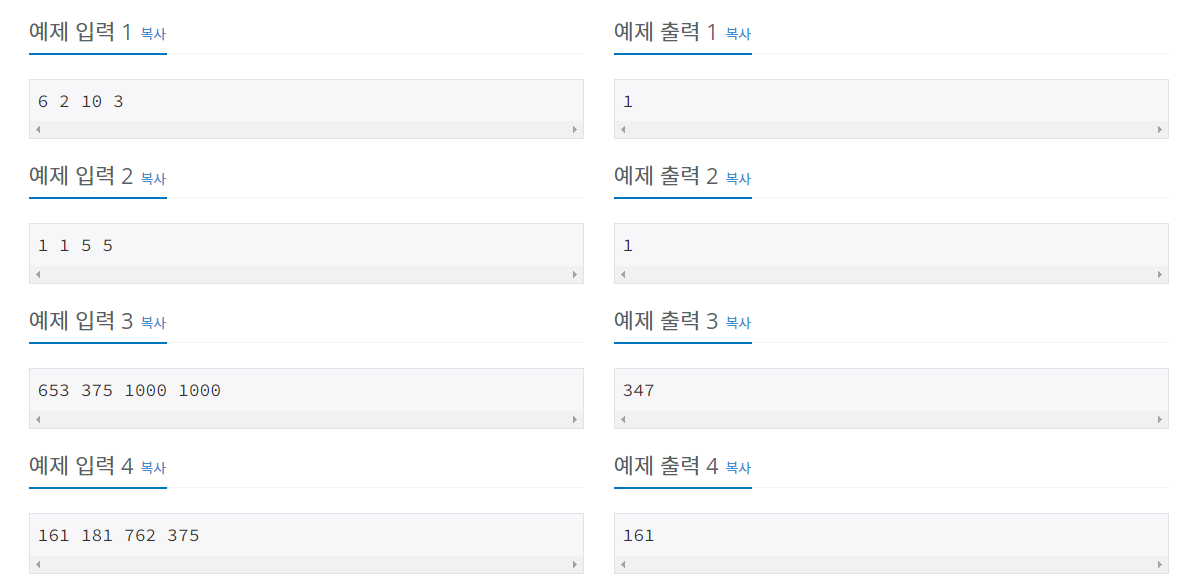
한수는 지금 (x, y)에 있다. 직사각형은 각 변이 좌표축에 평행하고, 왼쪽 아래 꼭짓점은 (0, 0), 오른쪽 위 꼭짓점은 (w, h)에 있다. 직사각형의 경계선까지 가는 거리의 최솟값을 구하는 프로그램
www.acmicpc.net

소스 코드 :
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <math.h>
double cal(double a, double b, double c, double d)
{
double sum = 0;
sum = pow(a - c, 2) + pow(b - d, 2);
return sqrt(sum);
}
int main()
{
double x, y, w, h = 0;
double min = 0;
scanf("%lf %lf %lf %lf", &x, &y, &w, &h);
if (x >= w / 2.0 && y >= h / 2.0)
{
min = cal(x, y, w, y);
if (min > cal(x, y, x, h))
min = cal(x, y, x, h);
}
else if (x >= w / 2.0 && y < h / 2.0)
{
min = cal(x, y, x, 0);
if (min > cal(x, y, w, y))
min = cal(x, y, w, y);
}
else if (x < w / 2.0 && y >= h / 2.0)
{
min = cal(x, y, 0, y);
if (min > cal(x, y, x, h))
min = cal(x, y, x, h);
}
else
{
min = cal(x, y, 0, y);
if (min > cal(x, y, x, 0))
min = cal(x, y, x, 0);
}
printf("%0.f", min);
return 0;
}
마무리 : 이 문제는 직사각형의 경계선까지 가는 거리의 최솟값을 구하는 문제이다. 위 코드를 보니 비효율적으로 보이는 면이 많다. 일단, 거리의 최솟값을 구하는 문제에서 점과 직선의거리를 구해야한다. 이 때 직각의 관계가 가장 짧다.그러므로 굳이 (x, y)와 (w, h)의 거리를 구할 필요가 없다.
(w, h)의 반을 구해서 x, y가 어느 위치에 있는지 알고 구하는 문제인데 앞에서 말했던 직각의 관계가 짧은 거리라는 것을 인지하지 못해 이렇게 구하게 되어버린 것이다.
즉, (x, y)를 기준으로 x=0, x=w, y=0, y=h 축까지의 길이를 구하고 짧은 거리를 구하면 되는 것이다.
'백준 > C' 카테고리의 다른 글
| 백준 2231번 : 분해합 [C] (0) | 2022.08.02 |
|---|---|
| 백준 4153번 : 직각삼각형 [C] (0) | 2022.08.02 |
| 백준 1157번 : 단어 공부 [C] (0) | 2022.07.27 |
| 백준 8958번 : OX퀴즈 [C] (0) | 2022.07.27 |
| 백준 3052번 : 나머지 [C] (0) | 2022.07.25 |



